手写数字识别

发表于 分类于 阅读次数： Waline： 本文字数： 10k 阅读时长 ≈ 9 分钟
重新用神经网络做一下之前的 project

使用 MLP 实现

设置

1
2
3
4
5
import tensorflow as tf
from tensorflow import keras
from keras.datasets import mnist
import matplotlib.pyplot as plt
tf.config.list_physical_devices('GPU')
[PhysicalDevice(name='/physical_device:GPU:0', device_type='GPU')]

载入数据

1
2
3
4
5
6
7
(x_train,y_train),(x_test,y_test) = mnist.load_data()

plt.figure()
plt.imshow(x_test[0])
plt.colorbar()
plt.grid(False)
plt.show()
载入数据

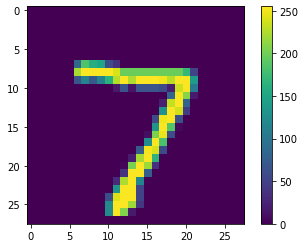
load_data()

返回：

两个元组：

x_train, x_test: uint8 数组表示的灰度图像，尺寸为 (num_samples, 28, 28)

y_train, y_test: uint8 数组表示的数字标签（范围在 0-9 之间的整数），尺寸为 (num_samples,)

参数： path: 如果在本地没有索引文件 (at '~/.keras/datasets/' + path), 它将被下载到该目录

Mnist 数据集

训练集为 60,000 张 28x28 像素灰度图像，测试集为 10,000 同规格图像，总共 10 类数字标签。

处理原始数据

1
2
3
4
5
6

x_train = x_train / 255.0       #隐式转换为float64
x_test = x_test / 255.0

print(x_train.shape,"train data")
print(x_test.shape,"test data")
(60000, 28, 28) train data
(10000, 28, 28) test data

将原始数据归一化。归一化的作用

转换标签

1
2
3
4
5
6
7
8
from keras.utils import to_categorical


y_train = to_categorical(y_train, num_classes=10)
y_test = to_categorical(y_test, num_classes=10)

print(y_test)

[[0. 0. 0. ... 1. 0. 0.]
 [0. 0. 1. ... 0. 0. 0.]
 [0. 1. 0. ... 0. 0. 0.]
 ...
 [0. 0. 0. ... 0. 0. 0.]
 [0. 0. 0. ... 0. 0. 0.]
 [0. 0. 0. ... 0. 0. 0.]]

使用 to_categorical() 将标签向量转化为 binary matrix

构建模型

1
2
3
4
5
6
7
8
9
10
11
12
13
from keras.models import Sequential
from keras.layers import Dense,Dropout,Flatten


model = Sequential()
model.add(Flatten(input_shape=(28,28)))
model.add(Dense(512,activation='relu',name="Dense1")) #添加全连接层
model.add(Dropout(0.3,name='dropout1'))
model.add(Dense(128,activation='relu',name='Dense2'))
model.add(Dropout(0.3,name='dropout2'))
model.add(Dense(10,activation='softmax',name='softmax'))
model.summary()

Model: "sequential"
_________________________________________________________________
Layer (type)                 Output Shape              Param #
=================================================================
flatten (Flatten)            (None, 784)               0
_________________________________________________________________
Dense1 (Dense)               (None, 512)               401920
_________________________________________________________________
dropout1 (Dropout)           (None, 512)               0
_________________________________________________________________
Dense2 (Dense)               (None, 128)               65664
_________________________________________________________________
dropout2 (Dropout)           (None, 128)               0
_________________________________________________________________
softmax (Dense)              (None, 10)                1290
=================================================================
Total params: 468,874
Trainable params: 468,874
Non-trainable params: 0
_________________________________________________________________

网络第一层 Flatten 将图像转换成以为数组，该层没有要学习的参数。

每个 Dense 层有 512 神经元， 最后一个使用 softmax 激活函数，它可以将一个数值向量归一化为一个概率分布向量:

\[ Softmax(zi) = \frac{e^{z_i}}{\sum_j {e^{z_j}}} \]

编译模型

1
2
3
4
5
6
from keras.losses import categorical_crossentropy
from keras.optimizers import Adamax

model.compile(optimizer=Adamax(),
              loss='categorical_crossentropy',
              metrics=['accuracy'])

使用 Admax 优化器，categotical_crossentropy（交叉熵损失） 作为损失函数，通常与 softmax 配合使用：

\[ Loss = -log(1-p_i) \]

\(p_i\)是预测样本真实标签得到的概率

训练模型

调用 model.fit 方法，这样命名因为会将模型与训练数据进行拟合

1
model.fit(x_train,y_train,batch_size=128,epochs=10,verbose=1,validation_data=(x_test,y_test))
Epoch 1/10
469/469 [==============================] - 4s 5ms/step - loss: 0.7144 - accuracy: 0.7838 - val_loss: 0.1901 - val_accuracy: 0.9447
Epoch 2/10
469/469 [==============================] - 2s 4ms/step - loss: 0.2355 - accuracy: 0.9317 - val_loss: 0.1319 - val_accuracy: 0.9605
Epoch 3/10
469/469 [==============================] - 2s 4ms/step - loss: 0.1644 - accuracy: 0.9515 - val_loss: 0.1056 - val_accuracy: 0.9678
Epoch 4/10
469/469 [==============================] - 2s 4ms/step - loss: 0.1290 - accuracy: 0.9617 - val_loss: 0.0917 - val_accuracy: 0.9717
Epoch 5/10
469/469 [==============================] - 2s 4ms/step - loss: 0.1077 - accuracy: 0.9687 - val_loss: 0.0837 - val_accuracy: 0.9743
Epoch 6/10
469/469 [==============================] - 2s 4ms/step - loss: 0.0963 - accuracy: 0.9710 - val_loss: 0.0751 - val_accuracy: 0.9759
Epoch 7/10
469/469 [==============================] - 2s 4ms/step - loss: 0.0802 - accuracy: 0.9763 - val_loss: 0.0738 - val_accuracy: 0.9772
Epoch 8/10
469/469 [==============================] - 2s 4ms/step - loss: 0.0714 - accuracy: 0.9790 - val_loss: 0.0663 - val_accuracy: 0.9791
Epoch 9/10
469/469 [==============================] - 2s 4ms/step - loss: 0.0664 - accuracy: 0.9798 - val_loss: 0.0647 - val_accuracy: 0.9798
Epoch 10/10
469/469 [==============================] - 2s 4ms/step - loss: 0.0570 - accuracy: 0.9830 - val_loss: 0.0633 - val_accuracy: 0.9800

epochs 是训练次数，validation_date 是划分出测试集，训练集正确率达到98%以上

评估准确率

1
2
3
test_loss,test_acc = model.evaluate(x_test,y_test,verbose=1)

print('\nTest accurancy', test_acc)
313/313 [==============================] - 1s 2ms/step - loss: 0.0284 - accuracy: 0.9916

Test accurancy 0.991599977016449

进行预测

来看第一个预测结果

1
2
3
4
5
import numpy as np

predictions= model.predict(x_test)
predictions[0]
np.argmax(predictions[0])
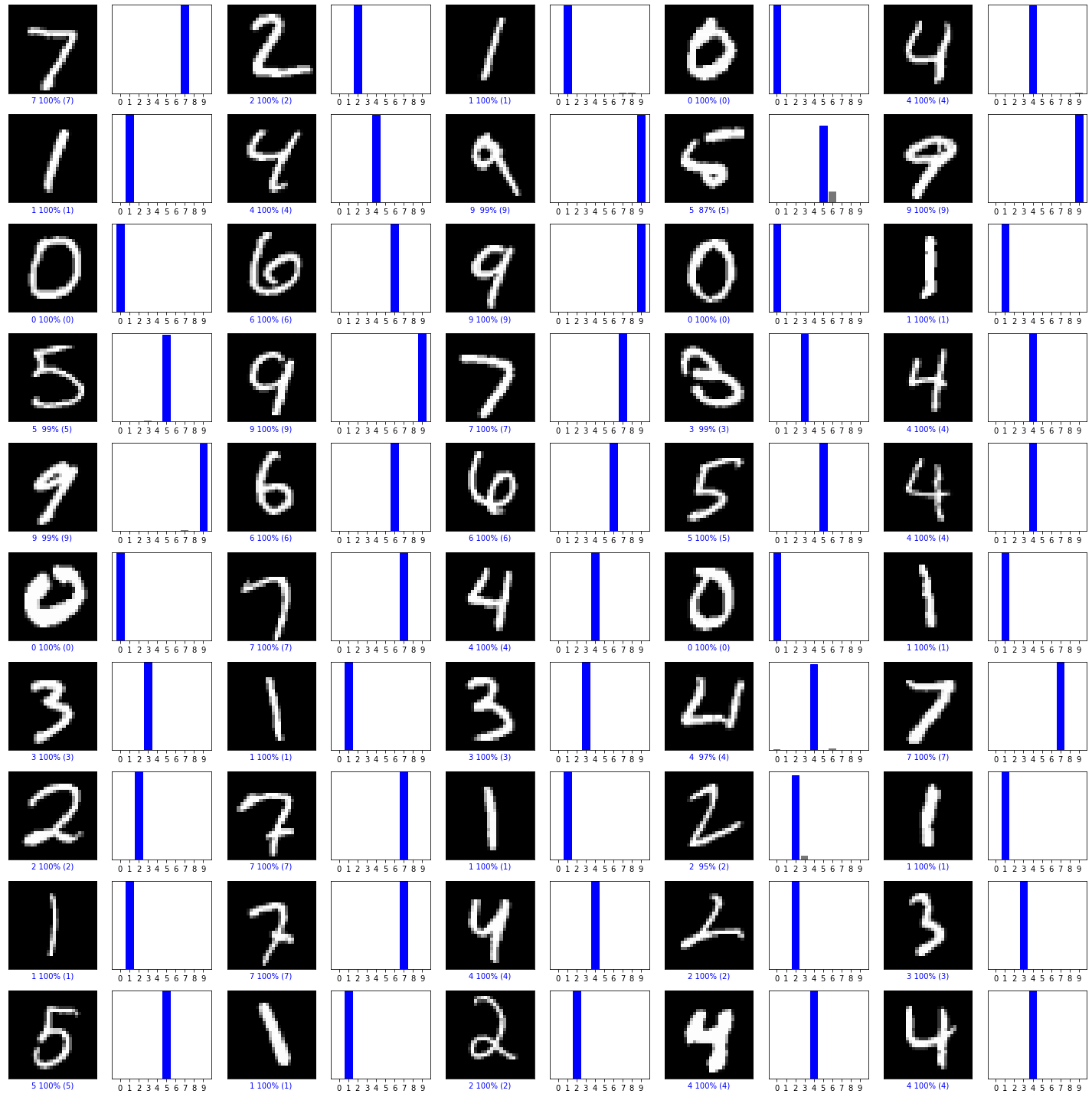
7

可以绘制图表，查看对全部类的预测

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
def plot_image(i,predictions_array, true_label, img):
  predictions_array, true_label, img = predictions_array, true_label, img
  plt.grid(False)
  plt.xticks([])
  plt.yticks([])

  plt.imshow(img, cmap='gray')

  predicted_label = np.argmax(predictions_array)

  if predicted_label == true_label:
    color = 'blue'
  else:
    color = 'red'

  plt.xlabel("{} {:3.0f}% ({})".format(predicted_label,
                                      100*np.max(predictions_array),true_label),color=color)

def plot_value_array(i,predictions_array, true_label):
   predictions_array, true_label = predictions_array, true_label
   plt.grid(False)
   plt.xticks(range(10))
   plt.yticks([])
   thisplot = plt.bar(range(10), predictions_array, color="#777777")
   plt.ylim([0,1])
   predicted_label = np.argmax(predictions_array)

   thisplot[predicted_label].set_color('red')
   thisplot[true_label].set_color('blue')

正确标签为蓝色，错误为红色

验证预测结果

1
2
3
4
5
6
7
8
9
10
11
12
13
num_rows = 10
num_cols = 5
num_images = num_rows*num_cols
plt.figure(figsize=(2*2*num_cols, 2*num_rows))
x_test.reshape(10000,28,28)
for i in range(num_images):
  t = np.argmax(y_test[i])
  plt.subplot(num_rows, 2*num_cols, 2*i+1)
  plot_image(i, predictions[i], t, x_test[i])
  plt.subplot(num_rows, 2*num_cols, 2*i+2)
  plot_value_array(i, predictions[i], t)
plt.tight_layout()
plt.show()
验证预测结果

使用 CNN

重新载入数据

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
(x_train,y_train),(x_test,y_test) = mnist.load_data()

plt.figure()
plt.imshow(x_test[0])
plt.colorbar()
plt.grid(False)
plt.show()

import numpy as np
x_train = np.expand_dims(x_train,-1)
x_test = np.expand_dims(x_test,-1)

x_train = x_train / 255.0
x_test = x_test / 255.0

y_train = to_categorical(y_train)
y_test = to_categorical(y_test)
载入数据

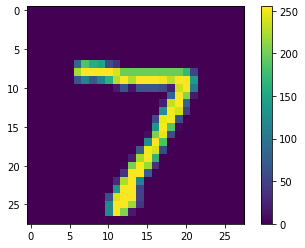
x.shape = (samples_nums, height, width, channels)

构建模型

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
from keras.layers import Conv2D,MaxPooling2D
model = Sequential()
input_size = (28,28,1)
model.add(Conv2D(32,
          kernel_size = (3,3), 
          activation = 'relu',
          input_shape = input_size))

model.add(Dropout(0.3))

model.add(Conv2D(16,
          kernel_size = (3,3), 
          activation = 'relu'))
model.add(MaxPooling2D(pool_size=(2,2)))
model.add(Dropout(0.3))
model.add(Flatten())
model.add(Dense(128,activation='relu'))
model.add(Dropout(0.4))
model.add(Dense(10,activation='softmax'))
model.summary()
Model: "sequential_5"
_________________________________________________________________
Layer (type)                 Output Shape              Param #
=================================================================
conv2d_8 (Conv2D)            (None, 26, 26, 32)        320
_________________________________________________________________
dropout_12 (Dropout)         (None, 26, 26, 32)        0
_________________________________________________________________
conv2d_9 (Conv2D)            (None, 24, 24, 16)        4624
_________________________________________________________________
max_pooling2d_4 (MaxPooling2 (None, 12, 12, 16)        0
_________________________________________________________________
dropout_13 (Dropout)         (None, 12, 12, 16)        0
_________________________________________________________________
flatten_5 (Flatten)          (None, 2304)              0
_________________________________________________________________
dense_8 (Dense)              (None, 128)               295040
_________________________________________________________________
dropout_14 (Dropout)         (None, 128)               0
_________________________________________________________________
dense_9 (Dense)              (None, 10)                1290
=================================================================
Total params: 301,274
Trainable params: 301,274
Non-trainable params: 0
_________________________________________________________________

编译和训练模型

选择 Adamdelta 作为优化器

1
2
3
4
5
6
7
from keras.optimizers import Adam
model.compile(optimizer=Adam(), loss = 'categorical_crossentropy', metrics=['accuracy'])
model.fit(x_train,y_train,
          batch_size=128,
          epochs=10,
          verbose=1,
          validation_data=(x_test,y_test))
Epoch 1/10
469/469 [==============================] - 6s 9ms/step - loss: 0.6243 - accuracy: 0.8000 - val_loss: 0.0790 - val_accuracy: 0.9767
Epoch 2/10
469/469 [==============================] - 3s 7ms/step - loss: 0.1273 - accuracy: 0.9605 - val_loss: 0.0503 - val_accuracy: 0.9837
Epoch 3/10
469/469 [==============================] - 3s 6ms/step - loss: 0.0927 - accuracy: 0.9715 - val_loss: 0.0396 - val_accuracy: 0.9874
Epoch 4/10
469/469 [==============================] - 3s 7ms/step - loss: 0.0748 - accuracy: 0.9758 - val_loss: 0.0387 - val_accuracy: 0.9891
Epoch 5/10
469/469 [==============================] - 3s 6ms/step - loss: 0.0634 - accuracy: 0.9814 - val_loss: 0.0355 - val_accuracy: 0.9880
Epoch 6/10
469/469 [==============================] - 3s 7ms/step - loss: 0.0558 - accuracy: 0.9828 - val_loss: 0.0331 - val_accuracy: 0.9900
Epoch 7/10
469/469 [==============================] - 3s 6ms/step - loss: 0.0502 - accuracy: 0.9835 - val_loss: 0.0295 - val_accuracy: 0.9911
Epoch 8/10
469/469 [==============================] - 3s 6ms/step - loss: 0.0488 - accuracy: 0.9848 - val_loss: 0.0296 - val_accuracy: 0.9906
Epoch 9/10
469/469 [==============================] - 3s 6ms/step - loss: 0.0439 - accuracy: 0.9856 - val_loss: 0.0313 - val_accuracy: 0.9910
Epoch 10/10
469/469 [==============================] - 3s 6ms/step - loss: 0.0420 - accuracy: 0.9865 - val_loss: 0.0303 - val_accuracy: 0.9912

<tensorflow.python.keras.callbacks.History at 0x16d0c5fa340>

评估准确率

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
test_loss, test_acc = model.evaluate(x_test, y_test, verbose= 2)

print('\nTest accuracy:', test_acc)

num_rows = 10
num_cols = 5
num_images = num_rows*num_cols
plt.figure(figsize=(2*2*num_cols, 2*num_rows))
x_test.reshape(10000,28,28)
for i in range(num_images):
  t = np.argmax(y_test[i])
  plt.subplot(num_rows, 2*num_cols, 2*i+1)
  plot_image(i, predictions[i], t, x_test[i])
  plt.subplot(num_rows, 2*num_cols, 2*i+2)
  plot_value_array(i, predictions[i], t)
plt.tight_layout()
plt.show()
313/313 - 1s - loss: 0.0303 - accuracy: 0.9912

Test accuracy: 0.9911999702453613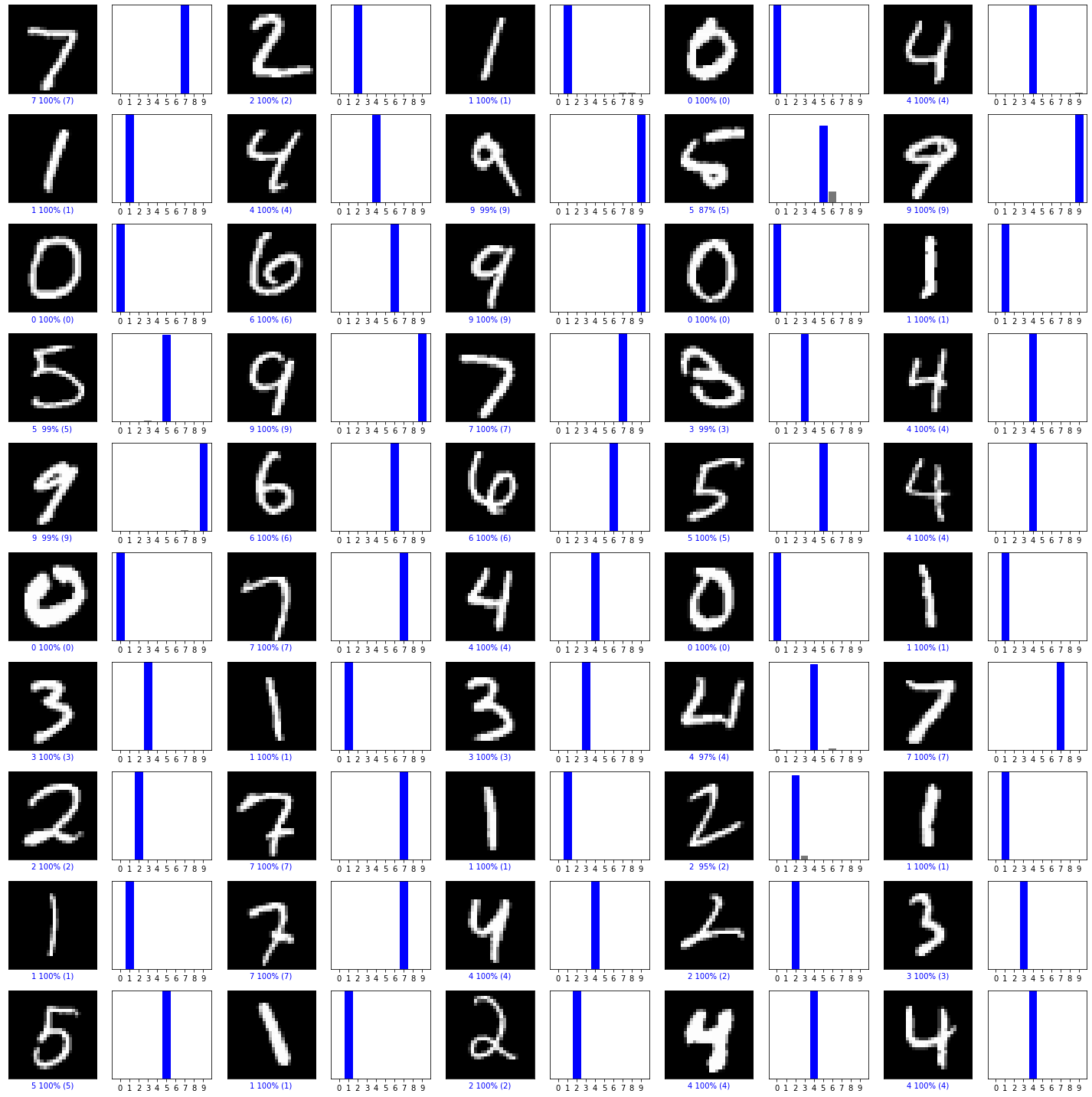
验证预测结果

CNN 与 MLP 对比

  1. CNN 能提取像素间的空间关系，而 MLP 将图像变为一维向量丢失空间信息
  2. MLP 是每一层是全连接的，参数数量多， CNN 每一层共享 kernel ，节点之间不是全连接，因此参数大小取决于 kernel 大小，参数数量少
  3. CNN　具有 局部平移不变性, 即无论图像出现在那个位置，都能提取到该特征。（因为共享 filter）. 而 MLP 不具有平移不变性，如果一张图片的特征出现在左上，而另一张特征出现在右下，那么 MLP 将尝试往右下修正参数。